About Regression

In simple terms, it’s like drawing a line through a scatter plot of data points to best represent the overall trend. And from the trend, the data points in future can be approximately predicted.

Same as the example mentioned previously:

e.g. To predict the price of housing in the future this is an example of supervised learning, because a dataset, the right answer that is the label or the right price on the plots, was provided to algorithm

How to represent

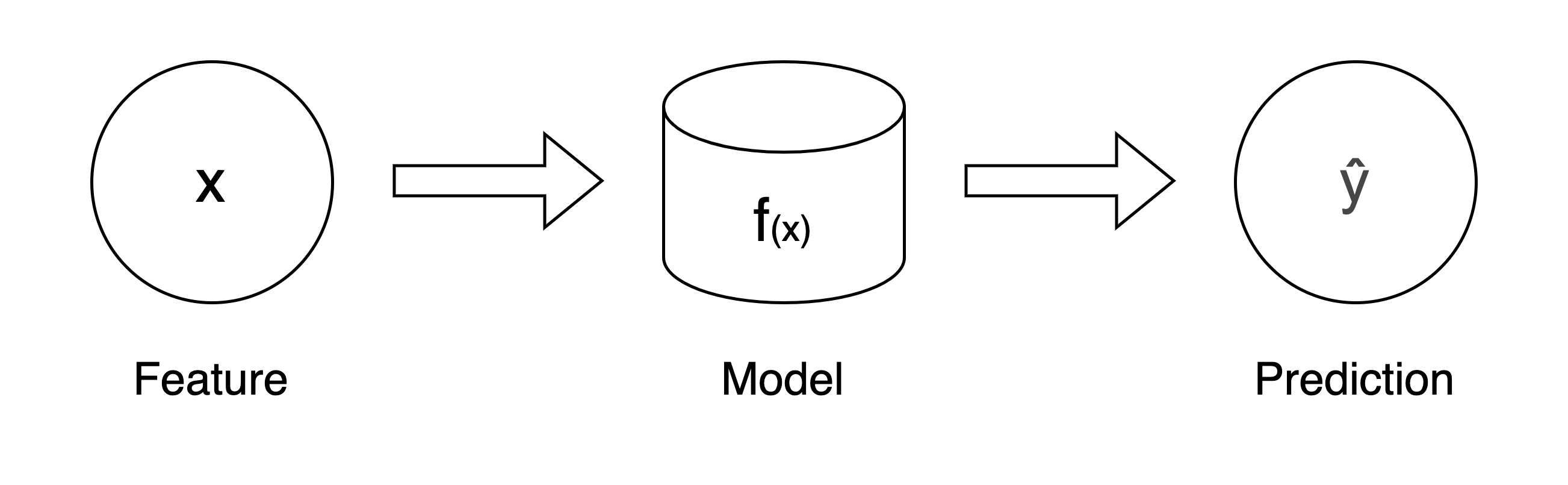
This is the diagram to show relationship between model, feature and prediction in use.

This is one of the examples of Linear Regression Function:

In the example given, it is an Univariate Linear Regression (Linear Regression with one variable). $f_{w,b}(x) = wx + b$ can be written as $f(x) = wx + b$ and $\hat{y} = wx + b$. Actually, $f(x)$ can be other functions like non-linear function such as curve or a parabola. the reason of using $f(x) = wx + b$ to represent Linear Regression is that linear function is relatively simple and easy to work with.

In a machine learning model, $w$ and $b$ are learned from the data during the training process to minimize the difference between the predicted values $\hat{y}$ and the actual values $y$.

Between $\hat{y}$ and $y$

The $y$ is the actual, observed, or true value from the data, while $\hat{y}$ (pronounced "y-hat") is the value predicted by the model. When $\hat{y}$ (the predicted value) gets closer and closer to $y$ (the actual value), it means that the model’s function $f(x)$ is making more accurate predictions.

In other words, the smaller the difference between $y$ and $\hat{y}$, the better the model is at capturing the true relationship between the input $x$ and the output $y$. This is often what we're aiming for in regression and other predictive modeling tasks—minimizing the difference (or error) between the actual outcomes and the predicted ones.

The only things that could be modified to make the prediction more accurate are $w$ and $b$. Changing the $w$ and $b$ variables in model to create a better line in order to reduce the error is the purpose.

But the question is that how to define the ERROR, the difference between the actual outcomes and the predicted ones, is getting smaller and smaller? More information will be involved in Loss Function.

Prediction Example

With the help of model, we can use it to make our original prediction. Let's predict the price of a house with 1200 sqft. Assume that the $x$ is 1.2.

1w = 200                         
2b = 100    
3x_i = 1.2
4cost_1200sqft = w * x_i + b    
5
6print(f"${cost_1200sqft:.0f} thousand dollars")