Home>study>artificial_intelligence>Machine_Learning_4_Loss_Function
2024-08-21
Machine Learning 4: Loss Function
童夢綺自習委員会

What is Loss Function

A loss function in machine learning is a mathematical function that measures the difference between the predicted output of a model (y^\hat{y}) and the actual output (or true label, yy). The purpose of the loss function is to quantify how well or poorly a model is performing by comparing the predicted values against the actual values.

Types of Loss Functions

There are different types of loss functions used depending on the type of machine learning problem. Mean Squared Error (MSE) will be an example to introduce, which measures the average squared difference between the predicted and actual values. It’s commonly used in regression problems.

MSE=1n∑i=1n(y^i−yi)2\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2

Example

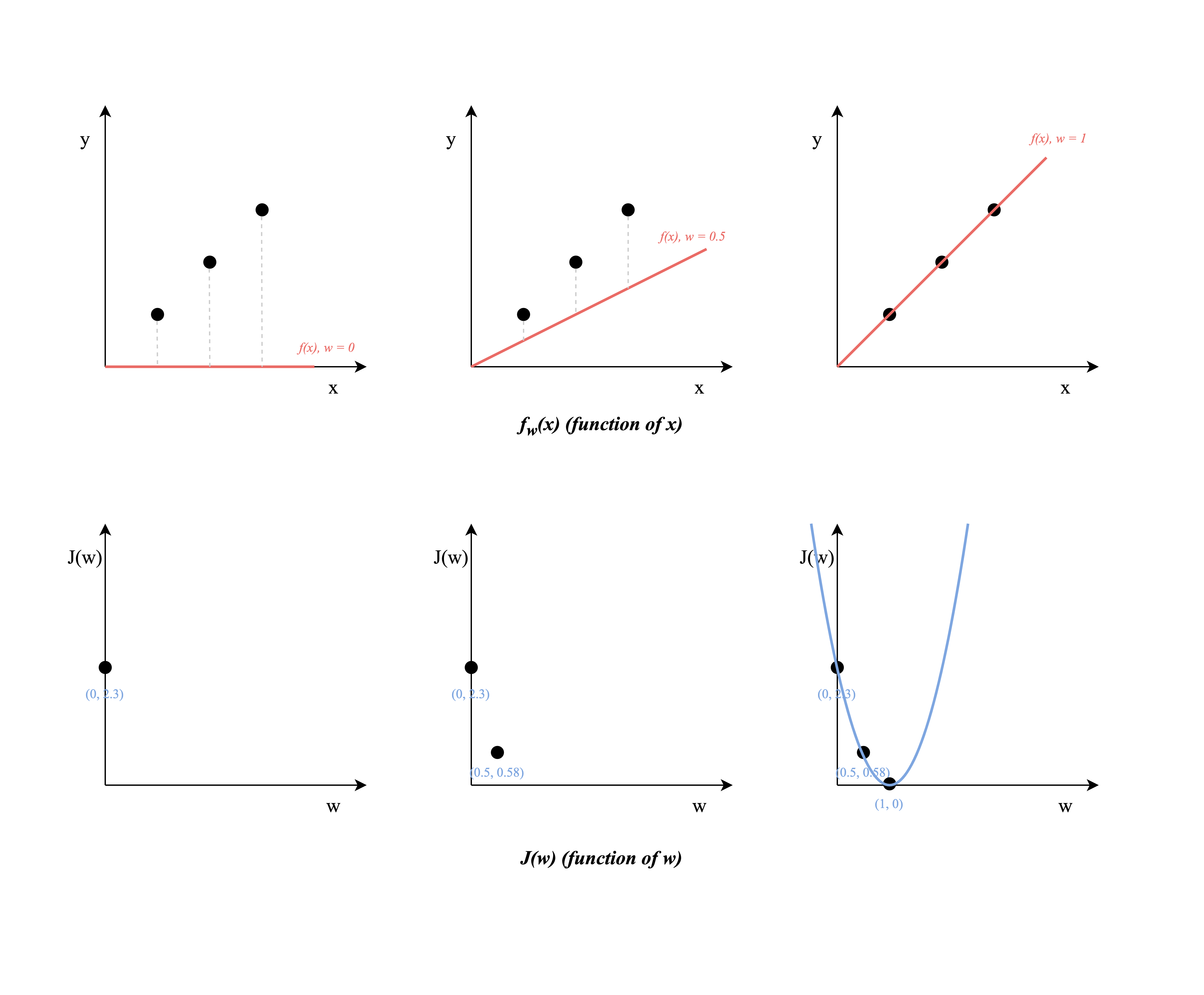
Assuming that the previous case of house price prediction will be discussed in detail. The model and cost function are given in the table below. In order to make it more clear and easy to understand, the bb has been assigned to 0. Therefore, function fw,b(x)=wx+bf_{w,b}(x) = wx + b has become to fw(x)=wxf_{w}(x) = wx

NameContent
Modelfw(x)=wxf_{w}(x) = wx
Parametersww
Cost FunctionJ(w)=1n∑i=1n(fw(xi)−yi)2J(w) = \frac{1}{n} \sum_{i=1}^{n} (f_{w}(x_i) - y_i)^2
GoalMinimizeJ(w)Minimize J(w)

Assume that there are three known data, which are (1,1)(1, 1), (2,2)(2, 2), and (3,3)(3, 3) if expressed in (x,y)(x, y). The input value is on the x-axis and the output value is on the y-axis. Then let ww equals to 0, 0.5 and 1 and do the further calculation (while ww can be any value).

The calculation detail:

∵J(w)=12n∑i=1n(wxi−yi)2,w=1\because J(w) = \frac{1}{2n} \sum_{i=1}^{n} (wx_i - y_i)^2, w = 1
∴J(0)=16∑i=13(xi−yi)2=(1−1)2+(2−2)2+(3−3)26=0\therefore J(0) = \frac{1}{6} \sum_{i=1}^{3} (x_i - y_i)^2 =\frac{(1 - 1)^2 + (2 - 2)^2 + (3 - 3)^2}{6} = 0
J(0.5)=16∑i=13(xi−yi)2=(0.5−1)2+(1−2)2+(1.5−3)26≈0.58J(0.5) = \frac{1}{6} \sum_{i=1}^{3} (x_i - y_i)^2 =\frac{(0.5 - 1)^2 + (1 - 2)^2 + (1.5 - 3)^2}{6} \approx 0.58
J(1)=16∑i=13(xi−yi)2=12+22+326≈2.3J(1) = \frac{1}{6} \sum_{i=1}^{3} (x_i - y_i)^2 =\frac{1^2 + 2^2 + 3^2}{6} \approx 2.3

The visualization of calculation result

Alt text for the image

What is other ways to calculate the w, instead of trying with numbers on by one. (Speculation)

Definition of the Loss Function

Assuming b=0b = 0, the loss function J(w)J(w) is defined as:

J(w)=1n∑i=1n(wxi−yi)2J(w) = \frac{1}{n} \sum_{i=1}^{n} \left( wx_i - y_i \right)^2

where n=3n = 3, because we have three data points.

Substituting Data Points

Substitute the data points (1,1)(1,1), (2,2)(2,2), and (3,3)(3,3) into the loss function:

J(w)=13[(w⋅1−1)2+(2w−2)2+(3w−3)2]J(w) = \frac{1}{3} \left[ (w \cdot 1 - 1)^2 + (2w - 2)^2 + (3w - 3)^2 \right]

This can be further simplified to:

J(w)=13[(w−1)2+(2w−2)2+(3w−3)2]J(w) = \frac{1}{3} \left[ (w - 1)^2 + (2w - 2)^2 + (3w - 3)^2 \right]

Taking the Derivative with Respect to ww

Differentiate with respect to ww and set the derivative to zero:

∂J(w)∂w=23[(w−1)⋅1+(2w−2)⋅2+(3w−3)⋅3]=0\frac{\partial J(w)}{\partial w} = \frac{2}{3} \left[ (w - 1) \cdot 1 + (2w - 2) \cdot 2 + (3w - 3) \cdot 3 \right] = 0

Expand and simplify:

∂J(w)∂w=23[(w−1)+4(w−1)+9(w−1)]=23×14×(w−1)=0\frac{\partial J(w)}{\partial w} = \frac{2}{3} \left[ (w - 1) + 4(w - 1) + 9(w - 1) \right] = \frac{2}{3} \times 14 \times (w - 1) = 0

Solving gives: w=1w = 1

Conclusion

The optimal value of ww is 11, so the ideal regression model (function) is: f(x)=1⋅xf(x) = 1 \cdot x